Una barca è in grado di navigare quando almeno la metà dei motori risulta funzionante. Supponiamo che ogni motore si possa guastare con probabilità \(p\) in modo indipendente dagli altri. Per quali valori di \(p\) un traghetto con quattro motori ha maggior probabilità di navigare di un traghetto con due motori?
L'idea è di trovare per quali \(p\) si ottiene che
\[\mathbb{P}(\text{navigare avendo 4 motori})\geq \mathbb{P}(\text{navigare avendo 2 motori})\]ovvero
\[ \mathbb{P}(\text{si rompono 0, 1, o 2 motori su 4})\geq \mathbb{P}(\text{si rompe 0 o 1 motore su 2})\]Possiamo modellare in generale lo scenario in cui ad una barca con \(n\) motori se ne rompano \(k\) impiegando una variabile aleatoria \(X\sim\text{Binomiale}(n,p)\) la cui densità
\[p(X=k) = {n\choose k}p^k(1-p)^{n-k} \]descrive la probabilità che di ottenere \(k\) successi (la rottura di \(k\) motori) nell'esecuzione di \(n\) esperimenti aleatori (l'avere \(n\) motori a disposizione) ciascuno dei quali può manifestare un successo con probabilità \(p\). In questo modo, il calcolo (2) si converte in
\[ \mathbb{P}(\text{Binomiale}(4,p) \leq 2) \geq \mathbb{P}(\text{Binomiale}(2,p) \leq 1) \]cioè
\[F_{\text{Binomiale}(4,p)}(2) \geq F_{\text{Binomiale}(2,p)}(1) \]dove \(F_X(t)\) è la funzione di ripartizione (cumulative distribution function, da cui la cdf che si vede nel codice) che descrive \(\mathbb{P}(X\leq t)\).
using Statistics, Distributions
using Plots
ps = range(0,1,length=1000)
p_navigare(k,p) = cdf(Binomial(k,p),div(k,2))
plot(ps,p_navigare.(2,ps), label="2 motori")
plot!(ps,p_navigare.(4,ps), label="4 motori")da cui notiamo come per \(p\leq 1/3\) la barca con 4 motori ha maggiori probabilità di navigare rispetto alla barca con 2 motori.
Questa è quindi la formulazione più comoda per il contesto informatico; altrimenti a mano converrebbe sommare i vari valori puntuali (cioè \(\mathbb{P}(X=k)\)) e lavorare da quelli la disequazione. Procedendo in questo modo infatti otterremo
\[ \mathbb{P}(\text{si rompono 0, 1, o 2 motori su 4})\geq \mathbb{P}(\text{si rompe 0 o 1 motore su 2}) \\ 1-\mathbb{P}(\text{si rompono 3 o 4 motori}) \geq 1-\mathbb{P}(\text{si rompono entrambi i motori}) \\ 1-{4\choose 3}p^3 (1-p)^1-p^4 \geq 1 - p^2 \\ -4p^3+4p^4-p^4 +p^2 \geq 0 \\ p^2(3p^2-4p+1)\geq 0 \\ 3p^2-4p +1 \geq 0 \implies p\in\left[0,\frac{1}{3}\right]\]Si potrebbero infine anche confrontare più motori ma l'idea è sempre la stessa: per \(p\) basse (i motori sono affidabili) sono avvantaggiate le barche con molti motori, dato che se anche se ne rompe qualcuno ce ne saranno spesso più della metà funzionanti. Al contrario, per \(p\) alte (un motore si guasta facilmente) diventa conveniente passare ad un modello con 2 soli motori, in modo da fornire in questo modo "meno occasioni" ai motori di manifestare un guasto.
plot(ps,p_navigare.(2,ps), label="2 motori")
plot!(ps,p_navigare.(4,ps), label="4 motori")
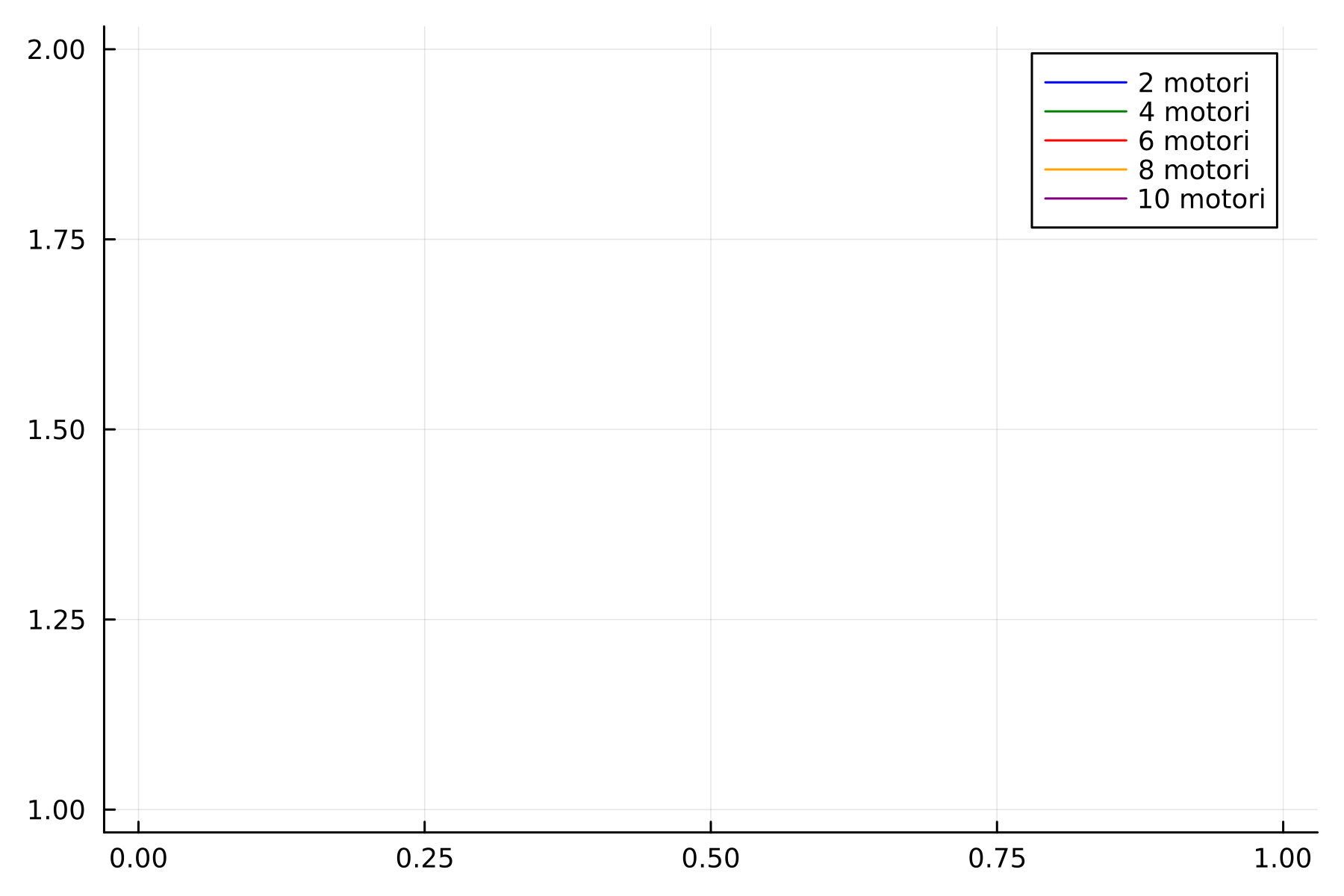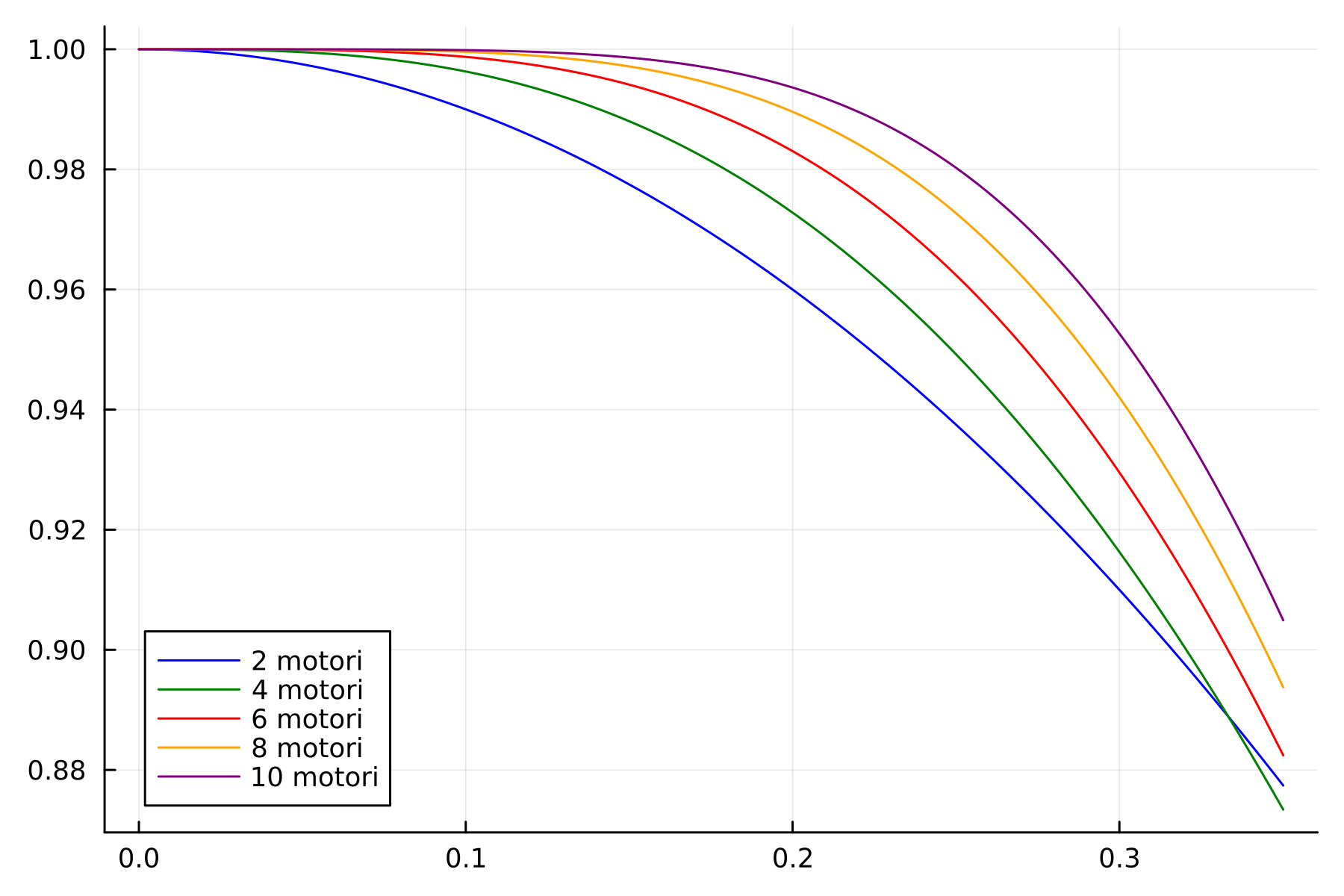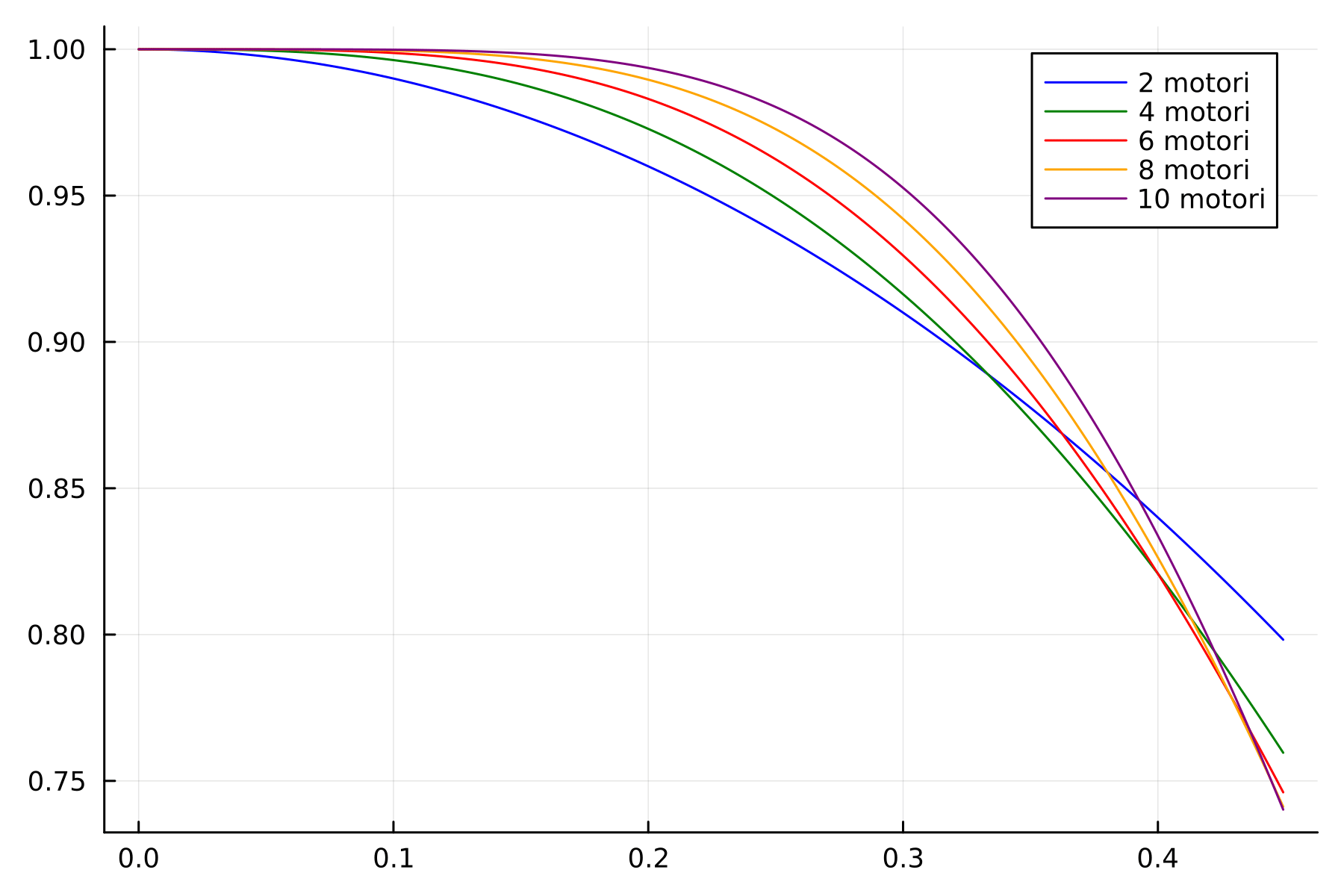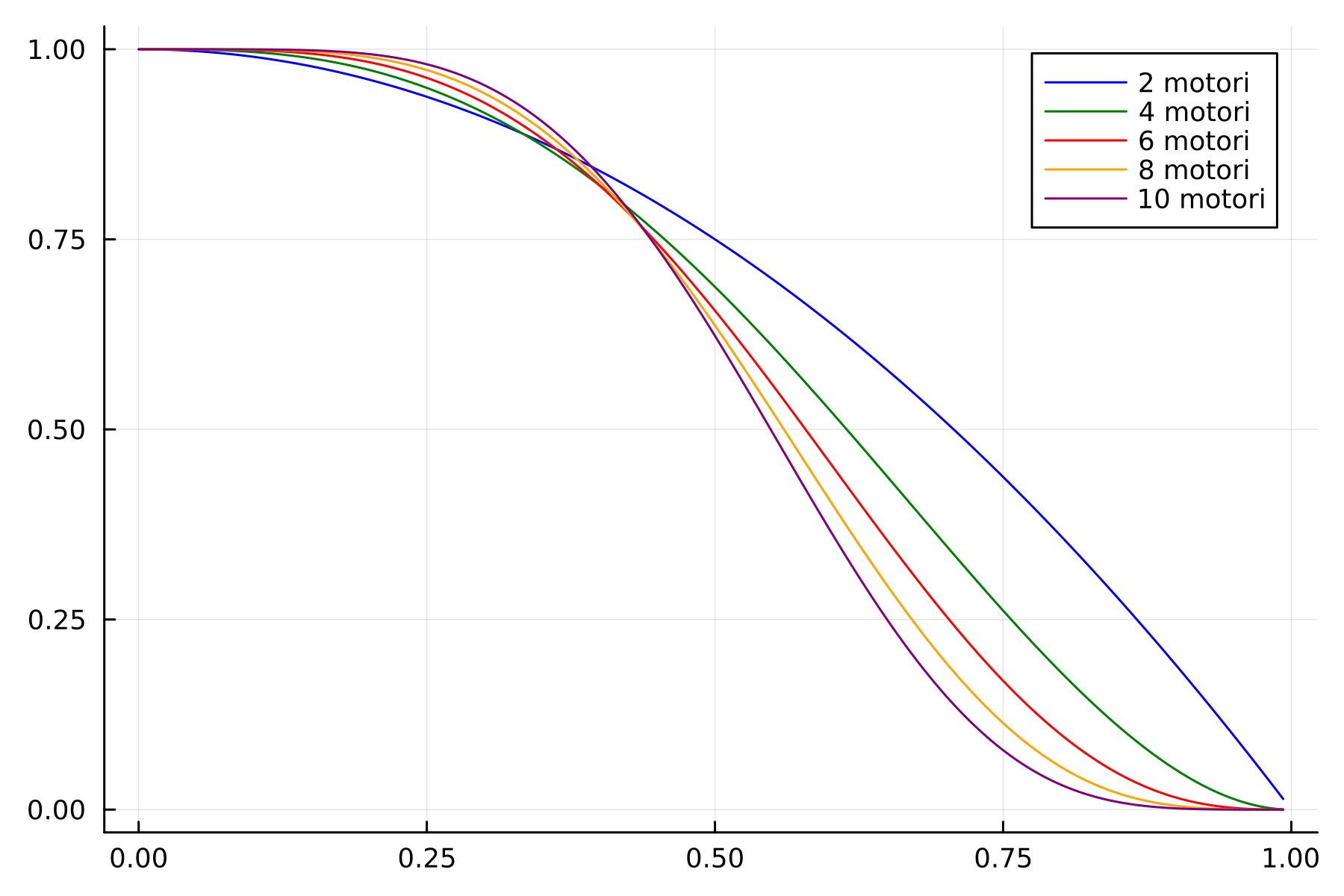
plot!(ps,p_navigare.(6,ps), label="6 motori")
plot!(ps,p_navigare.(8,ps), label="8 motori")
plot!(ps,p_navigare.(10,ps), label="10 motori")Concludiamo con una simpatica gif che mostra l'andamento delle varie probabilità, con anche un effetto Matrix/zoom nella parte centrale più interessante.
ps1 = range(0.0, 0.3, length=500) # less dense before 0.3
ps2 = range(0.3, 0.5, length=2000) # denser in [0.3, 0.5]
ps3 = range(0.5, 1.0, length=500) # less dense after 0.5
ps = unique(vcat(ps1, ps2, ps3))
ys = [p_navigare.(n, ps) for n in 2:2:10]
labels = string.(collect(2:2:10)," motori")
colors = [:blue, :green, :red, :orange, :purple]
@gif for i in 1:length(ps)
plt = plot(dpi=300)
for j in 1:length(ys)
plot!(ps[1:i], ys[j][1:i], label=labels[j], color=colors[j])
end
end every 10